Programación
Breve descripción de que es programación
Verdadero:El valor verdadero se representa con la letra V; si se emplea notación numérica se expresa con un uno: 1; en un circuito eléctrico, el circuito está cerrado.
↣El código fuente es escrito en un lenguaje de programación. El propósito de la programación es crear programas que exhiban un comportamiento deseado. El código fuente es escrito en un lenguaje de programación. El propósito de la programación es crear programas que exhiban un comportamiento deseado. El proceso de escribir códigos requiere frecuentemente conocimientos en varias áreas distintas, además del dominio del lenguaje a utilizar, algoritmos especializados y lógica formal. Programar no involucra necesariamente otras tareas tales como el análisis y diseño de la aplicación (pero sí el diseño del código), aunque sí suelen estar fusionadas en el desarrollo de pequeñas aplicaciones.↢
Está integrada por las siguientes unidades de estudio:
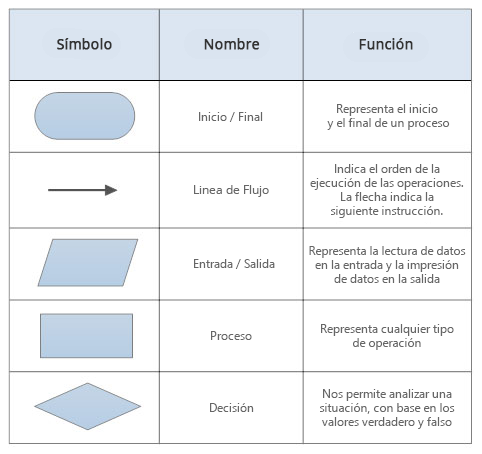
· Herramientas Lógicas: introduce al estudiante en la resolución de problemas matemáticos aplicados a la informática, la unidad de algoritmos y diagramas de flujo brinda al estudiante las herramientas básicas para resolución de problemas; que le permitirá al estudiante desarrollar las destrezas en planteamiento y análisis de problemas en una forma ordenada.
algoritmos; usan símbolos
conectados con flechas para indicar la secuencia de instrucciones.
Sistemas
numéricos
Herramientas
lógicas
Son
un conjunto de símbolos y reglas que se utilizan para
representar datos numéricos o cantidades. Se caracterizan por su base
que indican el número de símbolos distinto que utiliza y además es el
coeficiente que determina cual es el valor de cada símbolo
dependiendo de la posición que ocupe. Estas cantidades se caracterizan por
tener dígitos enteros y fraccionarios.
Sistema
decimal
Este
es el sistema que manejamos cotidianamente, está formado por diez símbolos {0,
1, 2, 3, 4, 5, 6, 7, 8, 9} por lo tanto la base del sistema es diez (10).
Sistema
binario
Es el sistema que utiliza internamente el hardware de las computadoras actuales, se basa en la representación de cantidades utilizando los dígitos 1 y 0. Por tanto su base es 2
video:https://www.youtube.com/watch?v=w-itbNvOG4A
Sistema
octalEl
sistema numérico octal utiliza ocho símbolos o dígitos para representar
cantidades y cifras numéricas. Los dígitos son: {0, 1, 2, 3, 4, 5, 6, 7}; la
base de éste es ocho (8) y es un sistema que se puede convertir directamente en
binario como se verá más adelante.
Sistema
HexadecimalEl sistema numérico hexadecimal utiliza
dieciséis dígitos y letras para representar cantidades y cifras numéricas. Los
símbolos son: {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F}; la base del
sistema es dieciséis (16).
Conversiones
De
Decimal a binario
DE
BINARIO A DECIMAL
↓
Se
eliminan los interruptores falsos o negativos y se suman todos los exponentes
de los dígitos positivos y el resultado de esto el número decimal.
CONVERSIÓN
DECIMAL – OCTAL ↓
Consiste en dividir un número y sus
sucesivos cocientes obtenidos por ocho hasta llegar a una división cuyo
cociente sea 0.
Octal
a decimal ↓
Existen varios métodos siendo el más
generalizado el indicado por el TFN (Teorema fundamental de la numeración) que
hace la conversión de forma directa por medio de la formula.
CONVERSIÓN
DE OCTAL A BINARIO ↓
Para convertir un numero octal a binario
se sustituye cada dígito octal en por sus correspondientes tres dígitos
binarios según la siguiente tabla. 
De
hexadecimal a decimal ↓
El método más utilizado es el TFN que nos
da el resultado por la aplicación directa de la formula.
OPERACIONES
ARITMÉTICAS
Suma de binarios
Multiplicación de binarios
La operación aritmética de multiplicar se
realiza del mismo modo que en el sistema numérico decimal.
•0*0 = 0
•0*1 = 0
•1*0 = 0
•1*1 = 1
Resta
de binarios
Se
utiliza la siguiente tabla:
0-0 =
0
1-0 =
1
0-1 =
1 y se acarrea 1, se toma como 11
1-1 =
0
División
de binarios
· Programación: tiene como finalidad que él o la estudiante conozca y domine el paradigma asociado a la programación estructurada, la lógica matemática para aplicarla a la resolución de problemas utilizando un lenguaje de programación.
¿Qué
es un Diagrama de flujo?
Los
diagramas de flujo son descripciones gráficas de
algoritmos; usan símbolos
conectados con flechas para indicar la secuencia de instrucciones.
Sistemas numéricos
Herramientas
lógicas
Son un conjunto de símbolos y reglas que se utilizan para representar datos numéricos o cantidades. Se caracterizan por su base que indican el número de símbolos distinto que utiliza y además es el coeficiente que determina cual es el valor de cada símbolo dependiendo de la posición que ocupe. Estas cantidades se caracterizan por tener dígitos enteros y fraccionarios.
Sistema decimal
Este es el sistema que manejamos cotidianamente, está formado por diez símbolos {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} por lo tanto la base del sistema es diez (10).
Sistema binario
Es el sistema que utiliza internamente el hardware de las computadoras actuales, se basa en la representación de cantidades utilizando los dígitos 1 y 0. Por tanto su base es 2
video:https://www.youtube.com/watch?v=w-itbNvOG4A
Sistema
octalEl
sistema numérico octal utiliza ocho símbolos o dígitos para representar
cantidades y cifras numéricas. Los dígitos son: {0, 1, 2, 3, 4, 5, 6, 7}; la
base de éste es ocho (8) y es un sistema que se puede convertir directamente en
binario como se verá más adelante.
Sistema
HexadecimalEl sistema numérico hexadecimal utiliza
dieciséis dígitos y letras para representar cantidades y cifras numéricas. Los
símbolos son: {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F}; la base del
sistema es dieciséis (16).
Conversiones
De
Decimal a binario
DE BINARIO A DECIMAL
↓
Se
eliminan los interruptores falsos o negativos y se suman todos los exponentes
de los dígitos positivos y el resultado de esto el número decimal.
CONVERSIÓN DECIMAL – OCTAL ↓
Consiste en dividir un número y sus sucesivos cocientes obtenidos por ocho hasta llegar a una división cuyo cociente sea 0.
Octal a decimal ↓
Existen varios métodos siendo el más generalizado el indicado por el TFN (Teorema fundamental de la numeración) que hace la conversión de forma directa por medio de la formula.
CONVERSIÓN DE OCTAL A BINARIO ↓
Para convertir un numero octal a binario se sustituye cada dígito octal en por sus correspondientes tres dígitos binarios según la siguiente tabla.
De hexadecimal a decimal ↓
El método más utilizado es el TFN que nos da el resultado por la aplicación directa de la formula.
OPERACIONES
ARITMÉTICAS
Suma de binarios
Multiplicación de binarios
La operación aritmética de multiplicar se
realiza del mismo modo que en el sistema numérico decimal.
•0*0 = 0
•0*1 = 0
•1*0 = 0
•1*1 = 1
Resta de binarios
Se
utiliza la siguiente tabla:
0-0 =
0
1-0 =
1
0-1 =
1 y se acarrea 1, se toma como 11
1-1 =
0
División de binarios
Conectivas lógicas
En lógica, una conectiva lógica, o simplemente conectiva, (también llamado operador lógico o conectores lógicos) es un símbolo o palabra que se utiliza para conectar dos fórmulas bien formadas o sentencias (atómicas o moleculares), de modo que el valor de verdad de la fórmula compuesta depende del valor de verdad de las fórmulas componentes.
Los conectivos lógicos más comunes son los conectivos binarios (también llamados conectivos diádicos) que unen dos frases, que pueden ser consideradas los operandos de la función. También es común considerar a la negación como un conectivo monádico
Las conectivas lógicas son, junto con los cuantificadores, las principales constantes lógicas de muchos sistemas lógicos, principalmente la lógica proposicional y la lógica de predicados.
En programación se utilizan para combinar valores de verdad y obtener nuevos valores que determinen el flujo de control de un algoritmo o programa.
Álgbra de Boole
Un álgebra de boole es un sistema de elementos B=(0,1) y los operadores Binarios (.) y (+) y (')
Propiedades: 1-Propiedad Conmutativa:A+B=B+A
2-Propiedad Distributiva:A*(B+C)=A*B+A*C
A+B*C=(A+B)*(A+C)
3-Elementos Neutros diferentes:A+0=A
A*1=A
4-Siempre existe el complemento de A,denominado A': A+A'=1
A*A'=0
Tabla de la verdad
Una tabla de verdad, o tabla de valores de verdad, es una tabla que muestra el valor de verdad de una proposición compuesta, para cada combinación de verdad que se pueda asignar
Negación: El valor de verdad de la negación es el contrario de la proposición negada.
P
¬ P
1
0
0
1
Disyunción: La disyunción solamente es falsa si lo son sus dos componentes.
P
Q
P∨ Q
1
1
1
1
0
1
0
1
1
0
0
0
Conjunción: Solamente si las componentes de la conjunción son ciertas, la conjunción es cierta.
P
Q
P ∧ Q
1
1
1
1
0
0
0
1
0
0
0
0
Condicional: El condicional solamente es falso cuando el antecedente es verdadero y el consecuente es falso. De la verdad no se puede seguir la falsedad.
P
Q
P→ Q
1
1
1
1
0
0
0
1
1
0
0
1
Bicondicional: El bicondicional solamente es cierto si sus componentes tienen el mismo valor de verdad.
P
Q
P↔ Q
1
1
1
1
0
0
0
1
0
0
0
1
Tabla de verdad
En lógica, una conectiva lógica, o simplemente conectiva, (también llamado operador lógico o conectores lógicos) es un símbolo o palabra que se utiliza para conectar dos fórmulas bien formadas o sentencias (atómicas o moleculares), de modo que el valor de verdad de la fórmula compuesta depende del valor de verdad de las fórmulas componentes.
Los conectivos lógicos más comunes son los conectivos binarios (también llamados conectivos diádicos) que unen dos frases, que pueden ser consideradas los operandos de la función. También es común considerar a la negación como un conectivo monádico
Las conectivas lógicas son, junto con los cuantificadores, las principales constantes lógicas de muchos sistemas lógicos, principalmente la lógica proposicional y la lógica de predicados.
En programación se utilizan para combinar valores de verdad y obtener nuevos valores que determinen el flujo de control de un algoritmo o programa.
Álgbra de Boole
Un álgebra de boole es un sistema de elementos B=(0,1) y los operadores Binarios (.) y (+) y (')
Propiedades: 1-Propiedad Conmutativa:A+B=B+A
2-Propiedad Distributiva:A*(B+C)=A*B+A*C
A+B*C=(A+B)*(A+C)
3-Elementos Neutros diferentes:A+0=A
A*1=A
4-Siempre existe el complemento de A,denominado A': A+A'=1
A*A'=0
Tabla de la verdad
Una tabla de verdad, o tabla de valores de verdad, es una tabla que muestra el valor de verdad de una proposición compuesta, para cada combinación de verdad que se pueda asignar
Negación: El valor de verdad de la negación es el contrario de la proposición negada.
Disyunción: La disyunción solamente es falsa si lo son sus dos componentes.
Conjunción: Solamente si las componentes de la conjunción son ciertas, la conjunción es cierta.
Condicional: El condicional solamente es falso cuando el antecedente es verdadero y el consecuente es falso. De la verdad no se puede seguir la falsedad.
Bicondicional: El bicondicional solamente es cierto si sus componentes tienen el mismo valor de verdad.
Tabla de verdad
Verdadero:El valor verdadero se representa con la letra V; si se emplea notación numérica se expresa con un uno: 1; en un circuito eléctrico, el circuito está cerrado.
Falso:El valor falso se representa con la letra F; si se emplea notación numérica se expresa con un cero: 0; en un circuito eléctrico, el circuito está abierto.
Variable:Para una variable lógica A, B, C, ... pueden ser verdaderas V, o falsas F, los operadores fundamentales se definen así:
Funciones Básicas
Video:https://www.youtube.com/watch?v=t_D-7j1Sbk8
Expresiones y Operadores
Expresiones:Una expresión es una combinación de operadores y operandos de cuya evaluación se obtiene un valor.
Operadores:Un operador es un carácter o una secuencia de caracteres.
Funciones Básicas
Video:https://www.youtube.com/watch?v=t_D-7j1Sbk8
Expresiones y Operadores
Expresiones:Una expresión es una combinación de operadores y operandos de cuya evaluación se obtiene un valor.
Operadores:Un operador es un carácter o una secuencia de caracteres.
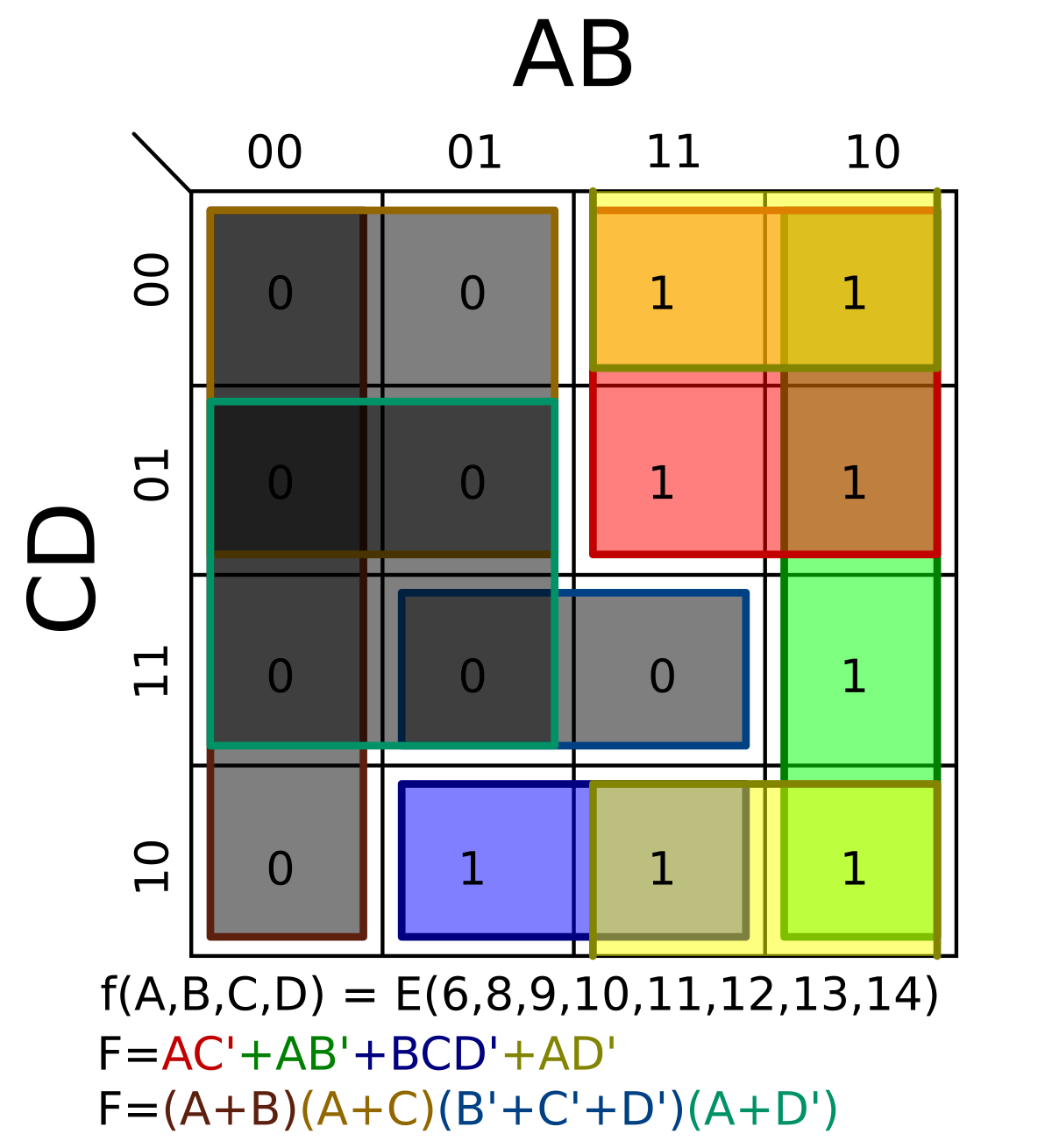
Reglas de simplificación
Las agrupaciones son exclusivas de unos. Esto implica que ningún grupo puede contener ningún cero.
Las agrupaciones únicamente puede hacerse en horizontal y vertical.
Los grupos han de contener 2 elementos
Cada grupo ha de ser tan grande como sea posible.
Todos los unos tienen que pertenecer como mínimo a un grupo.
Pueden existir solapamiento de grupos
La formación de grupos también se puede producir con las células extremas de la tabla.
Tiene que resultar el menor numero de grupos posibles,siempre y cuando no contradiga ninguna regla de las anteriores.
Matriz
En matemática, una matriz es un arreglo bidimensional de números. Dado que puede definirse tanto la suma como el producto de matrices, en mayor generalidad se dice que son elementos de un anillo. Una matriz se representa por medio de una letra mayúscula(A,B..) y sus elementos con la misma letra en minúscula (a,b...), con un doble subíndice donde el primero indica la fila y el segundo la columna a la que pertenece.
Propiedades de la suma de matrices:
1. Interna
La suma de dos matrices de orden m x n es otra matriz dimensión m x n.
2. Asociativa
A + (B + C) = (A + B) + C
3. Elemento neutro
A + 0 = A
Donde O es la matriz nula de la misma dimensión que la matriz A.
4. Elemento opuesto
A + (−A) = O
La matriz opuesta es aquella en que todos los elementos están cambiados de signo.
5. Conmutativa
A + B = B + A
RESTA:
El orden es igual que en la suma pero debes fijarte muy bien en los signos.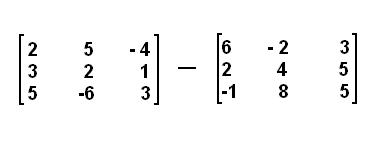
Multiplicación de matrices:
Para poder multiplicar debemos revisar primero el numero de filas x columnas.
Siempre se toma la primera matriz con la fila 1 (horizontal) con la 1 columna (Vertical) marcada en la matriz
Video:https://www.youtube.com/watch?v=eRBuGozq6Us
Reglas de simplificación
Las agrupaciones son exclusivas de unos. Esto implica que ningún grupo puede contener ningún cero.
Las agrupaciones únicamente puede hacerse en horizontal y vertical.
Los grupos han de contener 2 elementos
Cada grupo ha de ser tan grande como sea posible.
Todos los unos tienen que pertenecer como mínimo a un grupo.
Pueden existir solapamiento de grupos
La formación de grupos también se puede producir con las células extremas de la tabla.
Tiene que resultar el menor numero de grupos posibles,siempre y cuando no contradiga ninguna regla de las anteriores.
Matriz
En matemática, una matriz es un arreglo bidimensional de números. Dado que puede definirse tanto la suma como el producto de matrices, en mayor generalidad se dice que son elementos de un anillo. Una matriz se representa por medio de una letra mayúscula(A,B..) y sus elementos con la misma letra en minúscula (a,b...), con un doble subíndice donde el primero indica la fila y el segundo la columna a la que pertenece.
Propiedades de la suma de matrices:
Propiedades de la suma de matrices:
1. Interna
La suma de dos matrices de orden m x n es otra matriz dimensión m x n.
2. Asociativa
A + (B + C) = (A + B) + C
3. Elemento neutro
A + 0 = A
Donde O es la matriz nula de la misma dimensión que la matriz A.
4. Elemento opuesto
A + (−A) = O
La matriz opuesta es aquella en que todos los elementos están cambiados de signo.
5. Conmutativa
A + B = B + A
RESTA:
El orden es igual que en la suma pero debes fijarte muy bien en los signos.
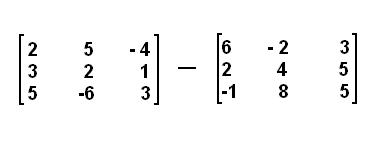
Multiplicación de matrices:
Para poder multiplicar debemos revisar primero el numero de filas x columnas.
Siempre se toma la primera matriz con la fila 1 (horizontal) con la 1 columna (Vertical) marcada en la matriz
Video:https://www.youtube.com/watch?v=eRBuGozq6Us
Comentarios
Publicar un comentario